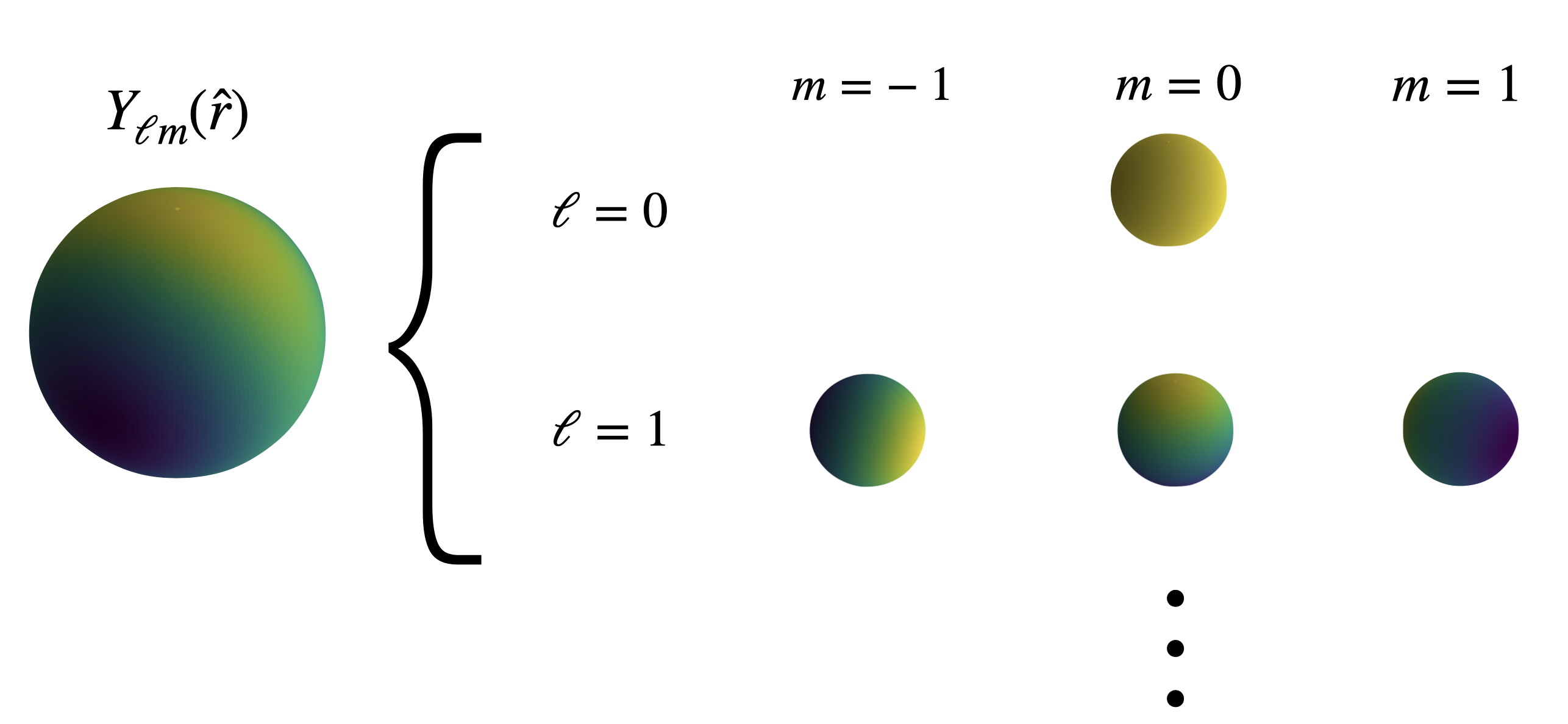
Computational breakthroughs for higher-order correlation functions
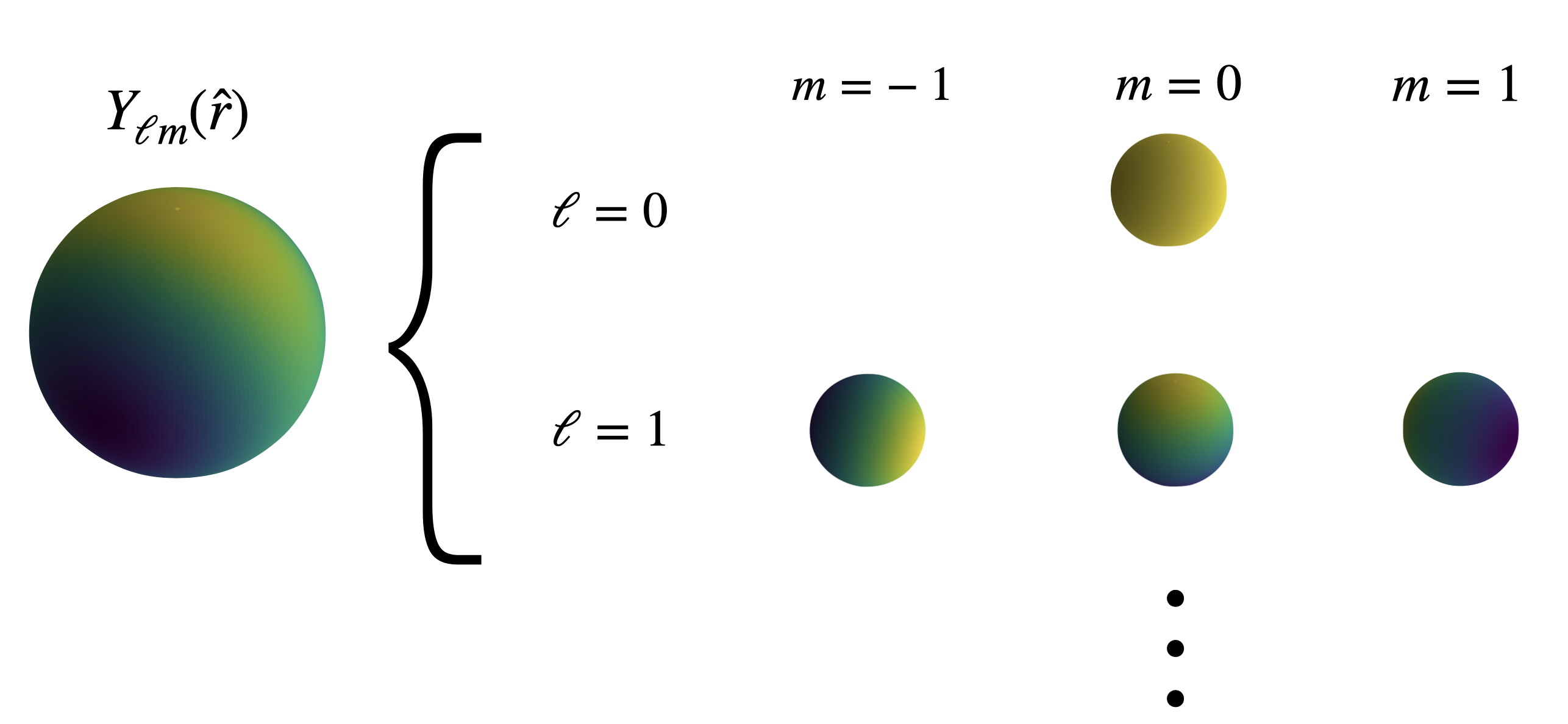
Spherical harmonics provide a natural and powerful basis for decomposing four-point functions in cosmology. Given the statistical isotropy of the Universe, it is essential to use a basis that respects rotational invariance. Each set of spherical harmonics spans a $(2\ell + 1)$-dimensional vector space, and tensor products of multiple such spaces decompose into a direct sum of irreducible representations labeled by total angular momentum $L$. The rotationally invariant singlet state ($L=0$) plays a key role in isolating isotropic contributions. In addition, spherical harmonics naturally separate into even and odd $\ell$, making them directly sensitive to parity transformations. Their factorizability further enables higher-order correlators to be reduced to products of pairwise computations, ensuring scalability to large datasets by significantly reducing computational cost.
Comparison of computational costs shows that spherical-harmonic-based N-point correlation function (NPCF) algorithms drastically outperform traditional brute-force approaches. In our benchmark studies, the dashed lines indicate a power-law extrapolation of the brute-force method, which would make NPCF calculations nearly infeasible for modern galaxy surveys. With GPU acceleration, computing the four-point function for millions of galaxies can be done in just a few minutes.
Related Publications: Philcox ++ JH ++ (2021), arXiv:2105.08722
Sunseri ++ JH ++ (2022), arXiv:2210.10206